Self-Organizing-MAP with MNIST data
Self-Organizing-MAP(SOM)
Suppose your mission is to cluster colors, images, or text. Unsupervised learning(no label information is provided) can handle such problems, and specifically for image clustering, one of the most widely used algorithms is Self-Organizing-MAP(SOM).
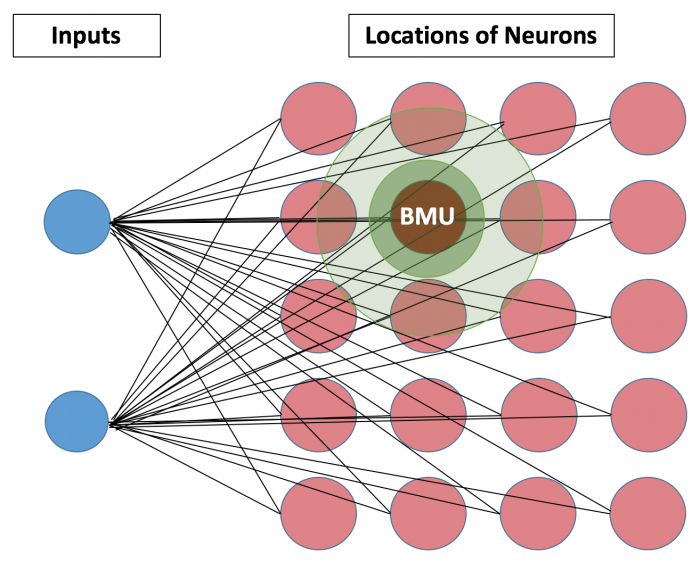
The ‘Map’ of SOM indicates the locations of neurons, which is different from the neuron graph of Artificial Neural Network(ANN). Based on this ‘locations’, SOM presumes that closely connected neurons and inputs share similar properties. Such closest neuron is denoted as Best Matching Unit(BMU), and calculated based on the Euclidean distance between the neuron and inputs. The below figure demonstrates a small network of 5*4 neurons. For each iteration, after BMU is determined, SOM calculates the weights of other units within BMU’s neighborhood(the size of the initial neighborhood is pre-determined). As iteration number increases, the length of neighborhood radius and learning rate can be set up to decrease.
Specific Algorithm
-
Once each neuron’s weights are initialized, every neuron is examined to calculate the distance to inputs(the length of inputs should be the same as that of neuron weights in order to calculate the distance).
-
A neuron that has the smallest distance will be chosen as Best Matching Unit(BMU) - aka winning neuron.
-
The radius of a neighborhood of the BMU starts from the specified value and shrinks as the iteration increases. Found Nodes inside of the neighborhood are getting similar by changing their weights
SOM with MNIST data
Sachin Joglekar’s blog has illustrated how SOM algorithm works and its implementation in Tensorflow. I will apply a little-modified class ‘SOM’ into MNIST data and examine how well SOM works.
import matplotlib.pyplot as plt
import numpy as np
import random as ran
## Applying SOM into Mnist data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data", one_hot=True)
def train_size(num):
x_train = mnist.train.images[:num,:]
y_train = mnist.train.labels[:num,:]
return x_train, y_train
x_train, y_train = train_size(100)
x_test, y_test = train_size(110)
x_test = x_test[100:110,:]; y_test = y_test[100:110,:]
def display_digit(num):
label = y_train[num].argmax(axis=0)
image = x_train[num].reshape([28,28])
plt.title('Example: %d Label: %d' % (num, label))
plt.imshow(image, cmap=plt.get_cmap('gray_r'))
plt.show()
display_digit(ran.randint(0, x_train.shape[0]))
# Import som class and train into 30 * 30 sized of SOM lattice
from som import SOM
som = SOM(30, 30, x_train.shape[1], 200)
som.train(x_train)
# Fit train data into SOM lattice
mapped = som.map_vects(x_train)
mappedarr = np.array(mapped)
x1 = mappedarr[:,0]; y1 = mappedarr[:,1]
index = [ np.where(r==1)[0][0] for r in y_train ]
index = list(map(str, index))
## Plots: 1) Train 2) Test+Train ###
plt.figure(1, figsize=(12,6))
plt.subplot(121)
# Plot 1 for Training only
plt.scatter(x1,y1)
# Just adding text
for i, m in enumerate(mapped):
plt.text( m[0], m[1],index[i], ha='center', va='center', bbox=dict(facecolor='white', alpha=0.5, lw=0))
plt.title('Train MNIST 100')
# Testing
mappedtest = som.map_vects(x_test)
mappedtestarr = np.array(mappedtest)
x2 = mappedtestarr[:,0]
y2 = mappedtestarr[:,1]
index2 = [ np.where(r==1)[0][0] for r in y_test ]
index2 = list(map(str, index2))
plt.subplot(122)
# Plot 2: Training + Testing
plt.scatter(x1,y1)
# Just adding text
for i, m in enumerate(mapped):
plt.text( m[0], m[1],index[i], ha='center', va='center', bbox=dict(facecolor='white', alpha=0.5, lw=0))
plt.scatter(x2,y2)
# Just adding text
for i, m in enumerate(mappedtest):
plt.text( m[0], m[1],index2[i], ha='center', va='center', bbox=dict(facecolor='red', alpha=0.5, lw=0))
plt.title('Test MNIST 10 + Train MNIST 100')
plt.show()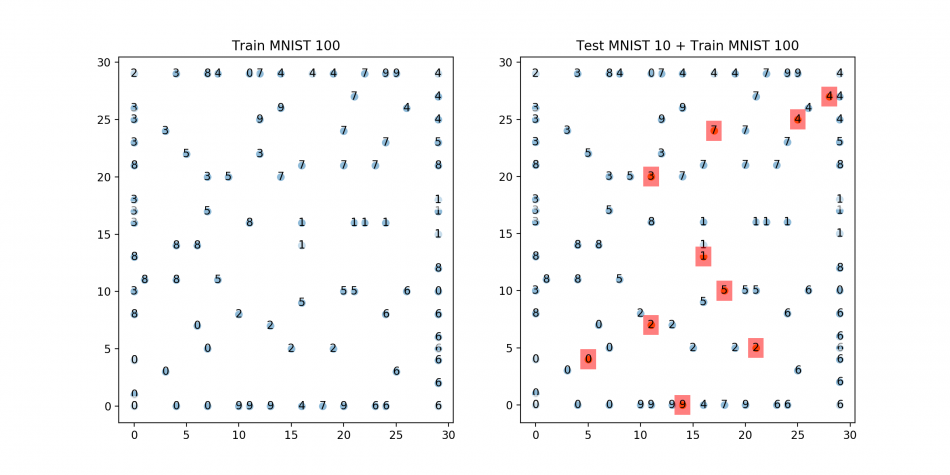
Each of the plotted MNIST test digits is well fitted into the target locations! Although digit 3 and 5 are not completely split, it seems to be resolved if the number of training iteration increases.
Within the SOM class written by Sachin, part of generating the location of BMU can generate an error because of data-type mismatch. To resolve it, you can change tf.constant type as int64(tf.int64) instead of int32 inside of tf.slice function.
bmu_loc = tf.reshape(tf.slice(self._location_vects, slice_input,
tf.constant(np.array([1, 2]), dtype=tf.int64) ), [2])import tensorflow as tf
import numpy as np
class SOM(object):
# To check if the SOM has been trained
trained = False
def __init__(self, m, n, dim, n_iterations=100, alpha=None, sigma=None):
# Assign required variables first
self.m = m; self.n = n
if alpha is None:
alpha = 0.2
else:
alpha = float(alpha)
if sigma is None:
sigma = max(m, n) / 2.0
else:
sigma = float(sigma)
self.n_iterations = abs(int(n_iterations))
self.graph = tf.Graph()
with self.graph.as_default():
# To save data, create weight vectors and their location vectors
self.weightage_vects = tf.Variable(tf.random_normal( [m * n, dim]) )
self.location_vects = tf.constant(np.array(list(self.neuron_locations(m, n))))
# Training inputs
# The training vector
self.vect_input = tf.placeholder("float", [dim])
# Iteration number
self.iter_input = tf.placeholder("float")
# Training Operation # tf.pack result will be [ (m*n), dim ]
bmu_index = tf.argmin(tf.sqrt(tf.reduce_sum(
tf.pow(tf.sub(self.weightage_vects, tf.pack(
[self.vect_input for _ in range(m * n)])), 2), 1)), 0)
slice_input = tf.pad(tf.reshape(bmu_index, [1]), np.array([[0, 1]]))
bmu_loc = tf.reshape(tf.slice(self.location_vects,
slice_input, tf.constant(np.array([1, 2]))), [2])
# To compute the alpha and sigma values based on iteration number
learning_rate_op = tf.sub(1.0, tf.div(self.iter_input, self.n_iterations))
alpha_op = tf.mul(alpha, learning_rate_op)
sigma_op = tf.mul(sigma, learning_rate_op)
# learning rates for all neurons, based on iteration number and location w.r.t. BMU.
bmu_distance_squares = tf.reduce_sum(tf.pow(tf.sub(
self.location_vects, tf.pack( [bmu_loc for _ in range(m * n)] ) ) , 2 ), 1)
neighbourhood_func = tf.exp(tf.neg(tf.div(tf.cast(
bmu_distance_squares, "float32"), tf.pow(sigma_op, 2))))
learning_rate_op = tf.mul(alpha_op, neighbourhood_func)
# Finally, the op that will use learning_rate_op to update the weightage vectors of all neurons
learning_rate_multiplier = tf.pack([tf.tile(tf.slice(
learning_rate_op, np.array([i]), np.array([1])), [dim]) for i in range(m * n)] )
### Strucutre of updating weight ###
### W(t+1) = W(t) + W_delta ###
### wherer, W_delta = L(t) * ( V(t)-W(t) ) ###
# W_delta = L(t) * ( V(t)-W(t) )
weightage_delta = tf.mul(
learning_rate_multiplier,
tf.sub(tf.pack([self.vect_input for _ in range(m * n)]), self.weightage_vects))
# W(t+1) = W(t) + W_delta
new_weightages_op = tf.add(self.weightage_vects, weightage_delta)
# Update weightge_vects by assigning new_weightages_op to it.
self.training_op = tf.assign(self.weightage_vects, new_weightages_op)
self.sess = tf.Session()
init_op = tf.global_variables_initializer()
self.sess.run(init_op)
def neuron_locations(self, m, n):
for i in range(m):
for j in range(n):
yield np.array([i, j])
def train(self, input_vects):
# Training iterations
for iter_no in range(self.n_iterations):
# Train with each vector one by one
for input_vect in input_vects:
self.sess.run(self.training_op,
feed_dict={self.vect_input: input_vect, self.iter_input: iter_no})
# Store a centroid grid for easy retrieval later on
centroid_grid = [[] for i in range(self.m)]
self.weightages = list(self.sess.run(self.weightage_vects))
self.locations = list(self.sess.run(self.location_vects))
for i, loc in enumerate(self.locations):
centroid_grid[loc[0]].append(self.weightages[i])
self.centroid_grid = centroid_grid
self.trained = True
def get_centroids(self):
if not self.trained:
raise ValueError("SOM not trained yet")
return self.centroid_grid
def map_vects(self, input_vects):
if not self.trained:
raise ValueError("SOM not trained yet")
to_return = []
for vect in input_vects:
min_index = min( [i for i in range(len(self.weightages))],
key=lambda x: np.linalg.norm(vect - self.weightages[x]) )
to_return.append(self.locations[min_index])
return to_return
